常见的二进位运算技巧

1. 位运算概述

从现代计算机中所有的数据二进制的形式存储在设备中。即 0、1 两种状态，计算机对二进制数据进行的运算(+、-、*、/)都是叫位运算，即将符号位共同参与运算的运算。

1
2
3
int a = 35;
int b = 47;
int c = a + b;

实际上运算如下: 计算两个数的和，因为在计算机中都是以二进制来进行运算，所以上面我们所给的 int 变量会在机器内部先转换为二进制在进行相加：

1
2
3
4
35:  0 0 1 0 0 0 1 1
47:  0 0 1 0 1 1 1 1
————————————————————
82:  0 1 0 1 0 0 1 0

所以，相比在代码中直接使用(+、-、*、/)运算符，合理的运用位运算更能显著提高代码在机器上的执行效率。

2. 位运算概览

位运算

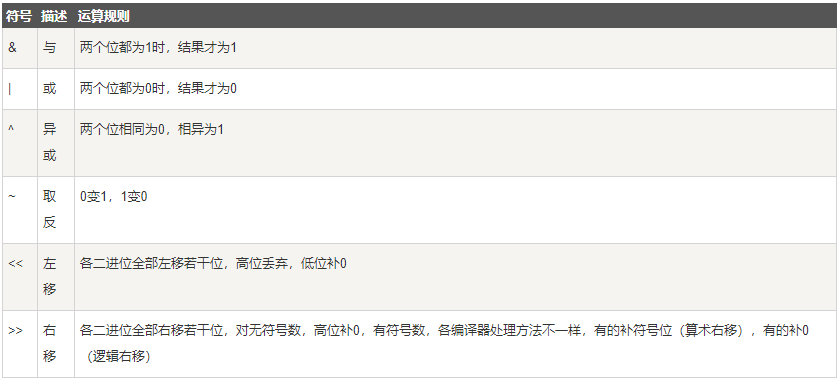
3. 按位与运算符

定义：参加运算的两个数据，按二进制位进行"与"运算。运算规则：

1
0&0=0  0&1=0  1&0=0  1&1=1

==总结：两位同时为1，结果才为1，否则结果为0。==

例如：3&5 即 0000 0011& 0000 0101 = 0000 0001，因此 3&5 的值得1。注意：负数按补码形式参加按位与运算。

与运算 & 的用途： 1）清零如果想将一个单元清零，即使其全部二进制位为0，只要与一个各位都为零的数值相与，结果为零。

2）取一个数的指定位比如取数 X=1010 1110 的低4位，只需要另找一个数Y，令Y的低4位为1，其余位为0，即Y=0000 1111，然后将X与Y进行按位与运算（X&Y=0000 1110）即可得到X的指定位。

3）判断奇偶只要根据最未位是0还是1来决定，为0就是偶数，为1就是奇数。因此可以用if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是不是偶数。

4. 异或运算符（^）

定义：参加运算的两个数据，按二进制位进行"异或"运算。

1
0^0=0  0^1=1  1^0=1  1^1=0

==总结：参加运算的两个对象，如果两个相应位相同为0，相异为1。==

异或的几条性质:

交换律
结合律 (a^b)^c == a^(b^c)
对于任何数x，都有 x^x=0，x^0=x
自反性: a^b^b=a^0=a;

与运算 ^ 的用途： 1）翻转指定位比如将数 X=1010 1110 的低4位进行翻转，只需要另找一个数Y，令Y的低4位为1，其余位为0，即Y=0000 1111，然后将X与Y进行异或运算（X^Y=1010 0001）即可得到。

2）与0相异或值不变例如：1010 1110 ^ 0000 0000 = 1010 1110

3）常见操作

1
2
3
4
5
6
7
a=0^a=a^0
0=a^a

由上面两个推导出：a=a^b^b

获取最后一个 1
diff=(n&(n-1))^n

4）交换两个数

1
2
3
4
5
void swap(int &a, int &b) {
  a ^= b;
  b ^= a;
  a ^= b;
}

5） n & n -1

1
2
3
4
5
6
7
8
9
移除最后一个 1
a=n&(n-1)

# 用 O(1) 时间检测整数 n 是否是 2 的幂次

N如果是2的幂次，则N满足两个条件。
1.N >0
2.N的二进制表示中只有一个1
因为N的二进制表示中只有一个1，所以使用N & (N - 1)将N唯一的一个1消去，应该返回0。

5. 左移运算符（«）

定义：将一个运算对象的各二进制位全部左移若干位（左边的二进制位丢弃，右边补0）。

设 a=1010 1110，a = a« 2 将a的二进制位左移2位、右补0，即得a=1011 1000。

若左移时舍弃的高位不包含1，则每左移一位，相当于该数乘以2。

6. 右移运算符（»）

定义：将一个数的各二进制位全部右移若干位，正数左补0，负数左补1，右边丢弃。

例如：a=a»2 将a的二进制位右移2位，左补0 或者左补1得看被移数是正还是负。

操作数每右移一位，相当于该数除以2。

应用

位操作统计二进制中 1 的个数

1
2
3
4
5
count = 0  
for a > 0{  
  a = a & (a - 1);  
  count++;  
}  

用一数组中，只有一个数出现一次，剩下都出现两次，找出出现一次的数

1
a := a^b^b

1. 位运算概述#

2. 位运算概览#

3. 按位与运算符#

4. 异或运算符（^）#

5. 左移运算符（«）#

6. 右移运算符（»）#

应用#