Summary

数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。由此可见，特征工程在机器学习中占有相当重要的地位。在实际应用当中，可以说特征工程是机器学习成功的关键。

什么是特征工程

特征工程又包含了Data PreProcessing（数据预处理）、Feature Extraction（特征提取）、Feature Selection（特征选择）和Feature construction（特征构造）等子问题，本章内容主要讨论数据预处理的方法及实现。特征工程是机器学习中最重要的起始步骤，数据预处理是特征工程的最重要的起始步骤，而数据清洗是数据预处理的重要组成部分，会直接影响机器学习的效果。

数据清洗整体介绍

data cleaning

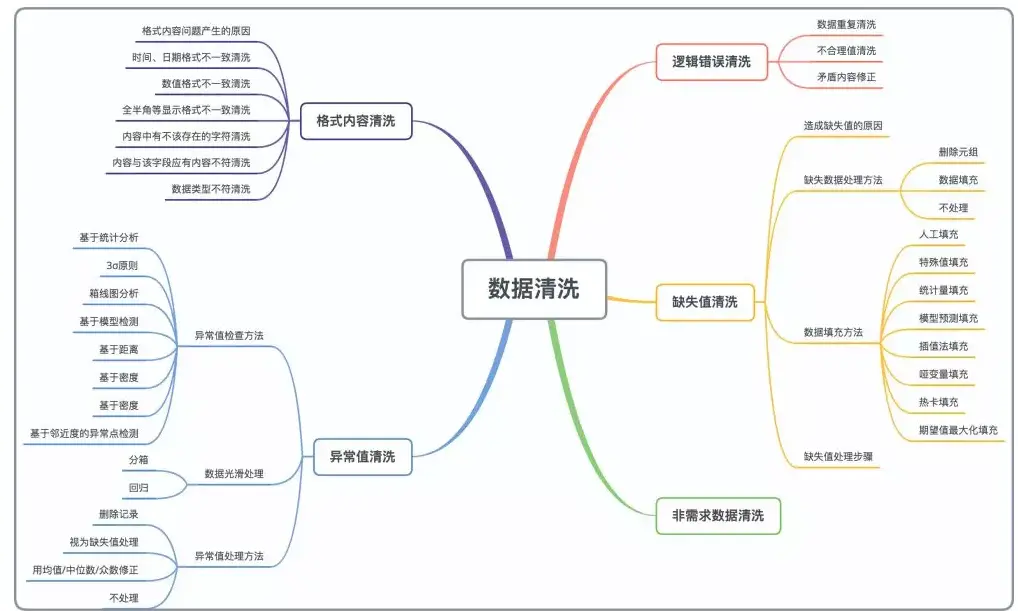
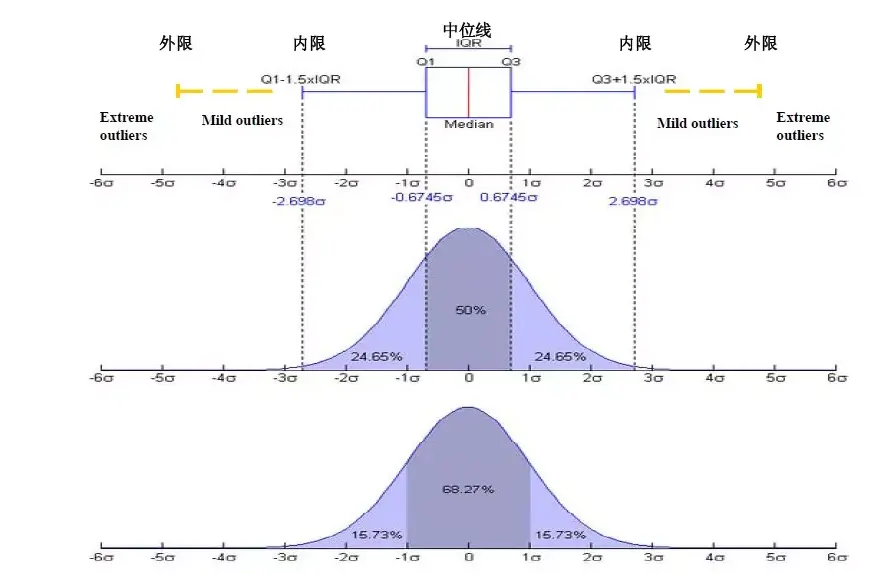
1. 箱线图分析异常值

箱线图提供了识别异常值的标准，如果一个数下雨 QL-1.5IQR or 大于OU + 1.5 IQR, 则这个值被称为异常值。

QL 下四分位数，表示四分之一的数据值比它小
QU　上四分位数，表示四分之一的数据值比它大
IRQ　四分位距，是QU－QL　的差值，包含了全部关差值的一般

箱线图展示

2. 数据的光滑处理

除了检测出异常值然后再处理异常值外，还可以使用以下方法对异常数据进行光滑处理。

2.1. 变量分箱（即变量离散化)

离散特征的增加和减少都很容易，易于模型的快速迭代；
稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；
特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。
可以将缺失作为独立的一类带入模型。
将所有变量变换到相似的尺度上。

2.1.0 变量分箱的方法

2.1.1 无序变量分箱

举个例子，在实际模型建立当中，有个 job 职业的特征，取值为（“国家机关人员”，“专业技术人员”，“商业服务人员”），对于这一类变量，如果我们将其依次赋值为（国家机关人员=1；专业技术人员=2；商业服务人员=3），就很容易产生一个问题，不同种类的职业在数据层面上就有了大小顺序之分，国家机关人员和商业服务人员的差距是2，专业技术人员和商业服务人员的之间的差距是1，而我们原来的中文分类中是不存在这种先后顺序关系的。所以这么简单的赋值是会使变量失去原来的衡量效果。

怎么处理这个问题呢? “一位有效编码” （one-hot Encoding）可以解决这个问题，通常叫做虚变量或者哑变量（dummpy variable）：比如职业特征有3个不同变量，那么将其生成个2哑变量，分别是“是否国家党政职业人员”，“是否专业技术人员” ，每个虚变量取值（1，0）。
为什么2个哑变量而非3个？在模型中引入多个虚拟变量时，虚拟变量的个数应按下列原则确定：
1. 回归模型有截距：一般的，若该特征下n个属性均互斥（如，男/女;儿童/青年/中年/老年），在生成虚拟变量时，应该生成 n-1个虚变量，这样可以避免产生多重共线性
2. 回归模型无截距项：有n个特征，设置n个虚拟变量
3. python 实现方法pd.get_dummies()

2.1.2 有序变量分箱

有序多分类变量是很常见的变量形式，通常在变量中有多个可能会出现的取值，各取值之间还存在等级关系。比如高血压分级（0=正常，1=正常高值，2=1级高血压，3=2级高血压，4=3级高血压）这类变量处理起来简直不要太省心，使用 pandas 中的 map（）替换相应变量就行。

1
2
3
4
5
import pandas as pd
df= pd.DataFrame(['正常','3级高血压','正常','2级高血压','正常','正常高值','1级高血压'],columns=['blood_pressure'])
dic_blood = {'正常':0,'正常高值':1,'1级高血压':2,'2级高血压':3,'3级高血压':4}
df['blood_pressure_enc'] = df['blood_pressure'].map(dic_blood)
print(df)

2.1.3 连续变量的分箱方式

等宽划分：按照相同宽度将数据分成几等份。缺点是受到异常值的影响比较大。 pandas.cut方法可以进行等宽划分。
等频划分：将数据分成几等份，每等份数据里面的个数是一样的。pandas.qcut方法可以进行等频划分。

1
2
3
4
5
6
import pandas as pd
df = pd.DataFrame([[22,1],[13,1],[33,1],[52,0],[16,0],[42,1],[53,1],[39,1],[26,0],[66,0]],columns=['age','Y'])
#print(df)
df['age_bin_1'] = pd.qcut(df['age'],3) #新增一列存储等频划分的分箱特征
df['age_bin_2'] = pd.cut(df['age'],3)  #新增一列存储等距划分的分箱特征
print(df)

2.1.4 有监督学习分箱方法

最小熵法分箱
- 假设因变量为分类变量，可取值1，… ，J。令pijpij表示第i个分箱内因变量取值为j的观测的比例，i=1，…，k，j=1，…，J；那么第i个分箱的熵值为∑Jj=0−pij×logpij∑j=0J−pij×logpij。如果第i个分箱内因变量各类别的比例相等，即p11=p12=p1J=1/Jp11=p12=p1J=1/J，那么第i个分箱的熵值达到最大值；如果第i个分箱内因变量只有一种取值，即某个pijpij等于1而其他类别的比例等于0，那么第i个分箱的熵值达到最小值。
- 令riri表示第i个分箱的观测数占所有观测数的比例；那么总熵值为∑ki=0∑Jj=0(−pij×logpij)∑i=0k∑j=0J(−pij×logpij)。需要使总熵值达到最小，也就是使分箱能够最大限度地区分因变量的各类别。
卡方分箱 (常用)
- 自底向上的(即基于合并的)数据离散化方法。
- 它依赖于卡方检验:具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。
- 基本思想:
  - 对于精确的离散化，相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并；否则，它们应当保持分开。而低卡方值表明它们具有相似的类分布。

2.2 无量纲化

无量纲化使不同规格的数据转换到同一规格。常见的无量纲化方法有标准化和区间缩放法。标准化的前提是特征值服从正态分布，标准化后，其转换成标准正态分布。区间缩放法利用了边界值信息，将特征的取值区间缩放到某个特点的范围，例如[0, 1]等。

2.2.1 标准化

标准化需要计算特征的均值和标准差，公式表达为：

　　使用preproccessing库的StandardScaler类对数据进行标准化的代码如下：

1
2
3
4
from sklearn.preprocessing import StandardScaler
 
#标准化，返回值为标准化后的数据
StandardScaler().fit_transform(iris.data)

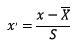
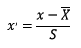
2.2.2 区间缩放法

　区间缩放法的思路有多种，常见的一种为利用两个最值进行缩放，公式表达为：

　　使用preproccessing库的MinMaxScaler类对数据进行区间缩放的代码如下：

1
2
3
4
from sklearn.preprocessing import MinMaxScaler

#区间缩放，返回值为缩放到[0, 1]区间的数据
MinMaxScaler().fit_transform(iris.data)

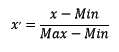
2.1.3 标准化与归一化的区别

简单来说，标准化是依照特征矩阵的列处理数据，其通过求z-score的方法，将样本的特征值转换到同一量纲下。归一化是依照特征矩阵的行处理数据，其目的在于样本向量在点乘运算或其他核函数计算相似性时，拥有统一的标准，也就是说都转化为“单位向量”。规则为l2的归一化公式如下：

什么时候需要进行归一化？

归一化后加快了梯度下降求最优解的速度
归一化有可能提高精度

什么时候需要进行归一化？

通常在需要用到梯度下降法的时候。

包括线性回归、逻辑回归、支持向量机、神经网络等模型。

决策树模型就不适用

例如 C4.5 ，主要根据信息增益比来分裂，归一化不会改变样本在特征 x 上的信息增益

比较概率大小分布即可，不需要。

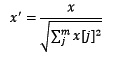
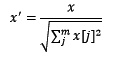
　　使用preproccessing库的Normalizer类对数据进行归一化的代码如下：

1
2
3
4
from sklearn.preprocessing import Normalizer

#归一化，返回值为归一化后的数据
Normalizer().fit_transform(iris.data)

2.3 对定量特征二值化

定量特征二值化的核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0，公式表达如下：

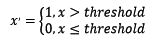
　　使用preproccessing库的Binarizer类对数据进行二值化的代码如下：

1
2
3
4
from sklearn.preprocessing import Binarizer

#二值化，阈值设置为3，返回值为二值化后的数据
Binarizer(threshold=3).fit_transform(iris.data)

2.4 对定性特征哑编码

由于IRIS数据集的特征皆为定量特征，故使用其目标值进行哑编码（实际上是不需要的）。使用preproccessing库的OneHotEncoder类对数据进行哑编码的代码如下：

1
2
3
4
from sklearn.preprocessing import OneHotEncoder

#哑编码，对IRIS数据集的目标值，返回值为哑编码后的数据
OneHotEncoder().fit_transform(iris.target.reshape((-1,1)))

2.5 缺失值计算

　由于IRIS数据集没有缺失值，故对数据集新增一个样本，4个特征均赋值为NaN，表示数据缺失。使用preproccessing库的Imputer类对数据进行缺失值计算的代码如下：

1
2
3
4
5
6
7
from numpy import vstack, array, nan
from sklearn.preprocessing import Imputer

#缺失值计算，返回值为计算缺失值后的数据
#参数missing_value为缺失值的表示形式，默认为NaN
#参数strategy为缺失值填充方式，默认为mean（均值）
Imputer().fit_transform(vstack((array([nan, nan, nan, nan]), iris.data)))

2.6 数据变换

常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。4个特征，度为2的多项式转换公式如下：

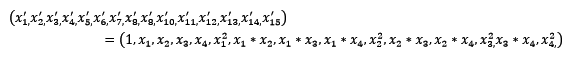
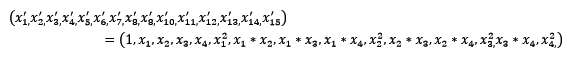
　　使用preproccessing库的PolynomialFeatures类对数据进行多项式转换的代码如下：

1
2
3
4
5
from sklearn.preprocessing import PolynomialFeatures

#多项式转换
#参数degree为度，默认值为2
PolynomialFeatures().fit_transform(iris.data)

基于单变元函数的数据变换可以使用一个统一的方式完成，使用preproccessing库的FunctionTransformer对数据进行对数函数转换的代码如下：

1
2
3
4
5
6
from numpy import log1p
from sklearn.preprocessing import FunctionTransformer

#自定义转换函数为对数函数的数据变换
#第一个参数是单变元函数
FunctionTransformer(log1p).fit_transform(iris.data)

2.7 回归

可以用一个函数（如回归函数）拟合数据来光滑数据。线性回归涉及找出拟合两个属性（或变量）的“最佳”线，是的一个属性可以用来预测另一个。多元线性回归是线性回归的扩展，其中涉及的属性多于两个，并且数据拟合到一个多维曲面。

3. 异常值处理方法

删除含有异常值的记录；
某些筛选出来的异常样本是否真的是不需要的异常特征样本，最好找懂业务的再确认一下，防止我们将正常的样本过滤掉了。
将异常值视为缺失值，交给缺失值处理方法来处理；
使用均值/中位数/众数来修正；
不处理。

4. 什么是组合特征？如何处理高维组合特征？

为了提高复杂关系的拟合能力，在特征工程中经常会把一阶离散特征两两组合成高阶特征，构成交互特征（Interaction Feature）。以广告点击预估问题为例，如图1所示，原始数据有语言和类型两种离散特征。为了提高拟合能力，语言和类型可以组成二阶特征。

5. 类别型特征

什么是类别型特征？

例如：性别（男、女）、血型（A、B、AB、O）

通常是字符串形式，需要转化成数值型，传递给模型

如何处理类别型特征？

序号编码（Ordinal Encoding）

例如学习成绩有高中低三档，也就是不同类别之间关系。

这时可以用321来表示，保留了大小关系。

独热编码（One-hot Encoding）

例如血型，它的类别没有大小关系。A 型血表示为（1, 0, 0, 0），B 型血表示为（0, 1, 0, 0）……

二进制编码（Binary Encoding）

第一步，先用序号编码给每个类别编码

第二步，将类别 ID 转化为相应的二进制

Summary#

什么是特征工程#

数据清洗整体介绍#

1. 箱线图分析异常值#

2. 数据的光滑处理#

2.1. 变量分箱（即变量离散化)#

2.1.0 变量分箱的方法#

2.1.1 无序变量分箱#

2.1.2 有序变量分箱#

2.1.3 连续变量的分箱方式#

2.1.4 有监督学习分箱方法#

最小熵法分箱#

卡方分箱 (常用)#

2.2 无量纲化#

2.2.1 标准化#

2.2.2 区间缩放法#

2.1.3 标准化与归一化的区别#

2.3 对定量特征二值化#

2.4 对定性特征哑编码#

2.5 缺失值计算#

2.6 数据变换#

2.7 回归#

3. 异常值处理方法#

4. 什么是组合特征？如何处理高维组合特征？#

5. 类别型特征#