介绍
FM和FMM模型在数据量比较大并且特征稀疏的情况下,仍然有优秀的性能表现,在CTR/CVR任务上尤其突出。
本文包括:
- FM 模型
- FFM 模型
- Deep FM 模型
- Deep FFM模型
FM模型的引入-广告特征的稀疏性
FM(Factorization machines)模型由Steffen Rendle于2010年提出,目的是解决稀疏数据下的特征组合问题。
在介绍FM模型之前,来看看稀疏数据的训练问题。
以广告CTR(click-through rate)点击率预测任务为例,假设有如下数据
| Clicked? | Country | Day | Ad_type |
|---|---|---|---|
| 1 | USA | 26/11/15 | Movie |
| 0 | China | 19/2/15 | Game |
| 1 | China | 26/11/15 | Game |
第一列Clicked是类别标记,标记用户是否点击了该广告,而其余列则是特征(这里的三个特征都是类别类型),一般的,我们会对数据进行One-hot编码将类别特征转化为数值特征,转化后数据如下:
| Clicked? | Country=USA | Country=China | Day=26/11/15 | Day=19/2/15 | Ad_type=Movie | Ad_type=Game |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 |
经过One-hot编码后,特征空间是十分稀疏的。特别的,某类别特征有m种不同的取值,则one-hot编码后就会被变为m维!当类别特征越多、类别特征的取值越多,其特征空间就更加稀疏。
此外,往往我们会将特征进行两两的组合,这是因为:
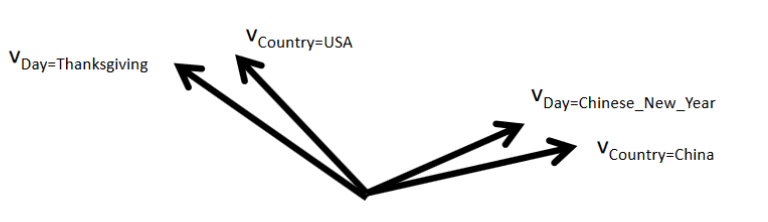
通过观察大量的样本数据可以发现,某些特征经过关联之后,与label之间的相关性就会提高。例如,“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征,对用户的点击有着正向的影响。换句话说,来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为,而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的,如“化妆品”类商品与“女”性,“球类运动配件”的商品与“男”性,“电影票”的商品与“电影”品类偏好等。
再比如,用户更常在饭点的时间下载外卖app,因此,引入两个特征的组合是非常有意义的。
如何表示两个特征的组合呢?一种直接的方法就是采用多项式模型来表示两个特征的组合,xixi为第ii个特征的取值(注意和以往表示第ii个样本的特征向量的区别),xixjxixj表示特征xixi和xjxj的特征组合,其系数wijwij即为我们学习的参数,也是xixjxixj组合的重要程度:
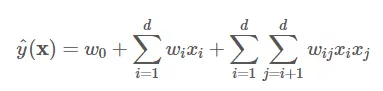
式1-1也可以称为Poly2(degree-2 poly-nomial mappings)模型。注意到式子1-1中参数的个数是非常多的!一次项有d+1个,二次项(即组合特征的参数)共有d(d−1)2d(d−1)2个,而参数与参数之间彼此独立,在稀疏场景下,二次项的训练是很困难的。因为要训练wijwij,需要有大量的xixi和xjxj都非零的样本(只有非零组合才有意义)。而样本本身是稀疏的,满足xixj≠0xixj≠0的样本会非常少,样本少则难以估计参数wijwij,训练出来容易导致模型的过拟合。
为此,Rendle于2010年提出FM模型,它能很好的求解式1-1,其特点如下:
- FM模型可以在非常稀疏的情况下进行参数估计
- FM模型是线性时间复杂度的,可以直接使用原问题进行求解,而且不用像SVM一样依赖支持向量。
- FM模型是一个通用的模型,其训练数据的特征取值可以是任意实数。而其它最先进的分解模型对输入数据有严格的限制。FMs可以模拟MF、SVD++、PITF或FPMC模型。
FM模型
前面提到过,式1-1的参数难以训练时因为训练数据的稀疏性。对于不同的特征对xi,xjxi,xj和xi,xkxi,xk,式1-1认为是完全独立的,对参数wijwij和wikwik分别进行训练。而实际上并非如此,不同的特征之间进行组合并非完全独立,如下图所示:
回想矩阵分解,一个rating可以分解为user矩阵和item矩阵,如下图所示:
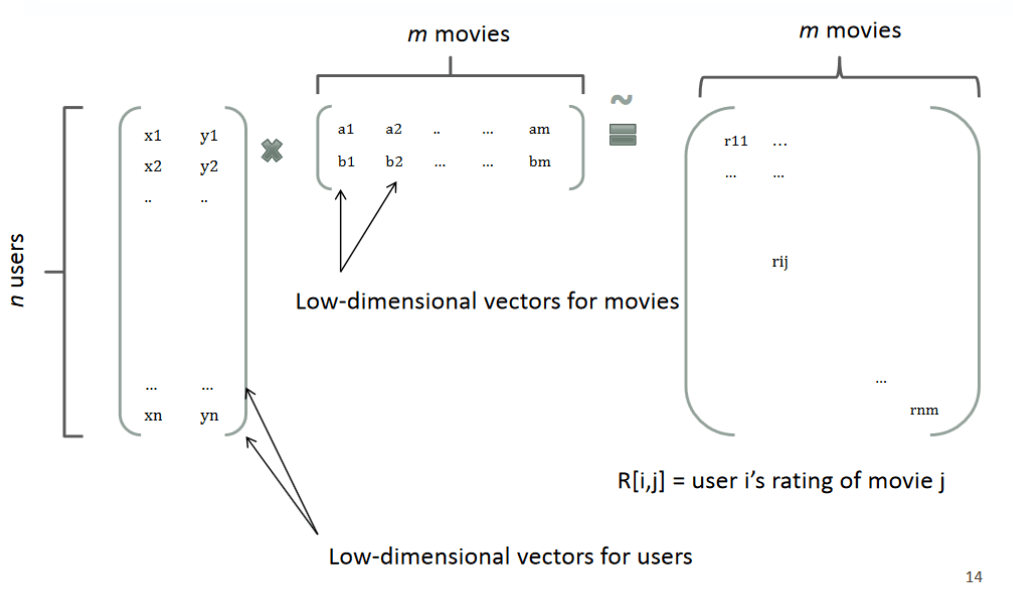
分解后得到user和item矩阵的维度分别为nknk和kmkm,(k一般由用户指定),相比原来的rating矩阵,空间占用得到降低,并且分解后的user矩阵暗含着user偏好,Item矩阵暗含着item的属性,而user矩阵乘上item矩阵就是rating矩阵中用户对item的评分。
因此,参考矩阵分解的过程,FM模型也将式1-1的二次项参数wijwij进行分解:
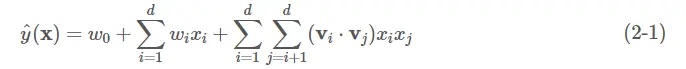
其中vivi是第ii维特征的隐向量,其长度为k(k≪d)k(k≪d)。 (vi⋅vj)(vi⋅vj)为内积,其乘积为原来的wijwij,即 ^wij=(vi⋅vj)=∑kf=1vi,f⋅vj,fw^ij=(vi⋅vj)=∑f=1kvi,f⋅vj,f
为了方便说明,考虑下面的数据集(实际中应该进行one-hot编码,但并不影响此处的说明):
| 数据集 | Clicked? | Publisher | Advertiser | Poly2参数 | FM参数 |
|---|---|---|---|---|---|
| 训练集 | 1 | NBC | Nike | wNBC,NikewNBC,Nike | VNBC⋅VNikeVNBC⋅VNike |
| 训练集 | 0 | EPSN | Adidas | wEPSN,AdidaswEPSN,Adidas | VEPSN⋅VAdidasVEPSN⋅VAdidas |
| 测试集 | ? | NBC | Adidas | wNBC,AdidaswNBC,Adidas | VNBC⋅VAdidas |
对于上面的训练集,没有(NBC,Adidas)组合,因此,Poly2模型就无法学习到参数wNBC,AdidaswNBC,Adidas。而FM模型可以通过特征组合(NBC,Nike)、(EPSN,Adidas) 分别学习到隐向量VNBCVNBC和VAdidasVAdidas,这样使得在测试集中得以进行预测。
更一般的,经过分解,式2-1的参数个数减少为kdkd个,对比式1-1,参数个数大大减少。使用小的k,使得模型能够提高在稀疏情况下的泛化性能。此外,将wijwij进行分解,使得不同的特征对不再是完全独立的,而它们的关联性可以用隐式因子表示,这将使得有更多的数据可以用于模型参数的学习。比如xi,xjxi,xj与xi,xkxi,xk的参数分别为:⟨vi,vj⟩⟨vi,vj⟩和⟨vi,vk⟩⟨vi,vk⟩,它们都可以用来学习vivi,更一般的,包含xixj≠0&i≠jxixj≠0&i≠j的所有样本都能用来学习vivi,很大程度上避免了数据稀疏性的影响。
此外,式2-1的复杂度可以从O(kd2)O(kd2)优化到O(kd)O(kd):
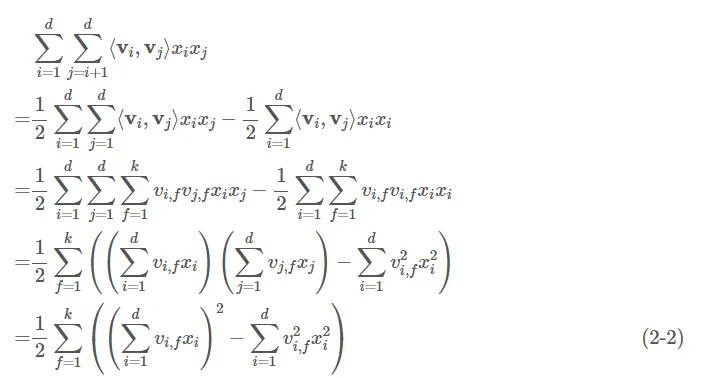
可以看出,FM模型可以在线性的时间做出预测。
FM模型学习

在2-4式中,∑dj=1vj,fxj∑j=1dvj,fxj只与ff有关而与ii无关,在每次迭代过程中,可以预先对所有ff的∑dj=1vj,fxj∑j=1dvj,fxj进行计算,复杂度O(kd)O(kd),就能在常数时间O(1)O(1)内得到vi,fvi,f的梯度。而对于其它参数w0w0和wiwi,显然也是在常数时间内计算梯度。此外,更新参数只需要O(1)O(1), 一共有1+d+kd1+d+kd个参数,因此FM参数训练的复杂度也是O(kd)O(kd)。
所以说,FM模型是一种高效的模型,是线性时间复杂度的,可以在线性的时间做出训练和预测。
FFM模型
考虑下面的数据集:
| Clicked? | Publisher(P) | Advertiser(A) | Gender(G) |
|---|---|---|---|
| 1 | EPSN | Nike | Male |
| 0 | NBC | Adidas | Female |
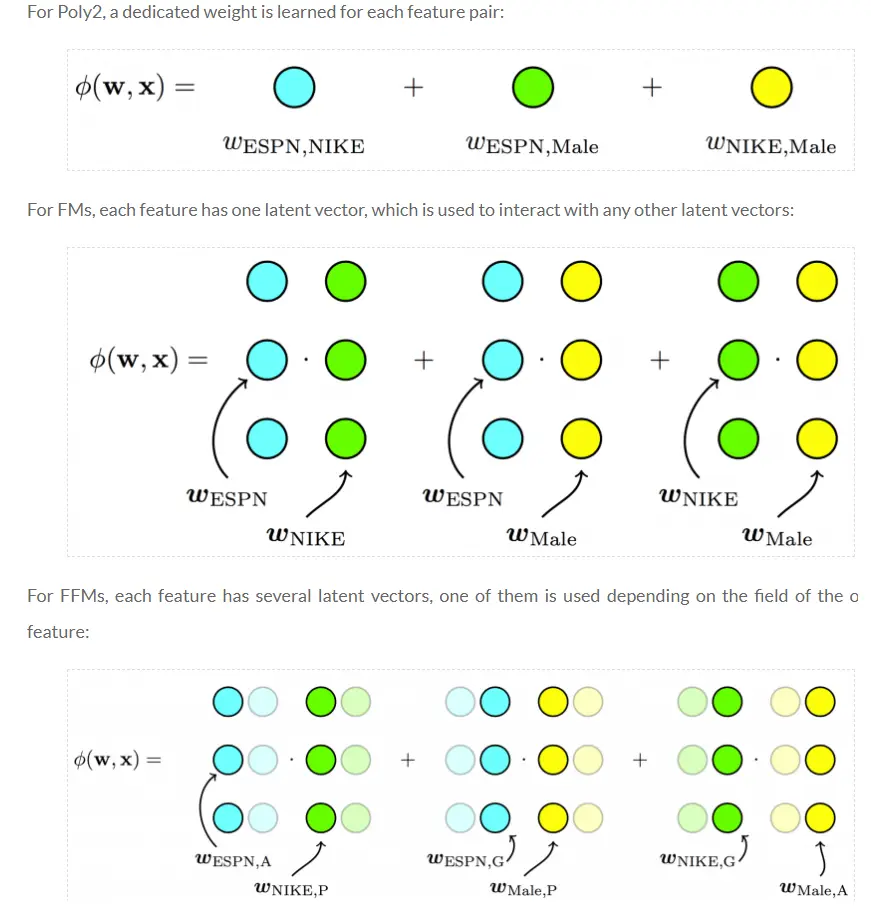
对于第一条数据来说,FM模型的二次项为:wEPSN⋅wNike+wEPSN⋅wMale+wNike⋅wMalewEPSN⋅wNike+wEPSN⋅wMale+wNike⋅wMale。(这里只是把上面的v符合改成了w)每个特征只用一个隐向量来学习和其它特征的潜在影响。对于上面的例子中,Nike是广告主,Male是用户的性别,描述(EPSN,Nike)和(EPSN,Male)特征组合,FM模型都用同一个wESPNwESPN,而实际上,ESPN作为广告商,其对广告主和用户性别的潜在影响可能是不同的。
因此,Yu-Chin Juan借鉴Michael Jahrer的论文(Ensemble of collaborative filtering and feature engineered models for click through rate prediction),将field概念引入FM模型。
field是什么呢?即相同性质的特征放在一个field。比如EPSN、NBC都是属于广告商field的,Nike、Adidas都是属于广告主field,Male、Female都是属于性别field的。简单的说,同一个类别特征进行one-hot编码后生成的数值特征都可以放在同一个field中,比如最开始的例子中Day=26/11/15 Day=19/2/15可以放于同一个field中。如果是数值特征而非类别,可以直接作为一个field。
引入了field后,对于刚才的例子来说,二次项变为:
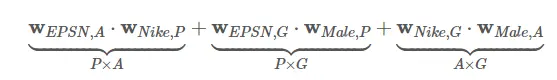
- 对于特征组合(EPSN,Nike)来说,其隐向量采用的是wEPSN,AwEPSN,A和wNike,PwNike,P,对于wEPSN,AwEPSN,A这是因为Nike属于广告主(Advertiser)的field,而第二项wNike,PwNike,P则是EPSN是广告商(Publisher)的field。
- 再举个例子,对于特征组合(EPSN,Male)来说,wEPSN,GwEPSN,G 是因为Male是用户性别(Gender)的field,而第二项wMale,PwMale,P是因为EPSN是广告商(Publisher)的field。
下面的图来自criteo,很好的表示了三个模型的区别
FFM 数学公式
因此,FFM的数学公式表示为:
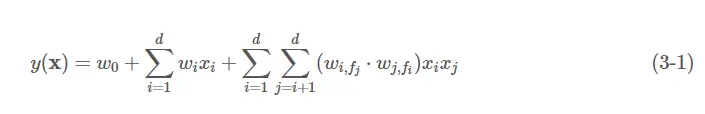
其中fifi和fjfj分别代表第i个特征和第j个特征所属的field。若field有ff个,隐向量的长度为k,则二次项系数共有dfkdfk个,远多于FM模型的dkdk个。此外,隐向量和field相关,并不能像FM模型一样将二次项化简,计算的复杂度是d2kd2k。
通常情况下,每个隐向量只需要学习特定field的表示,所以有kFFM≪kFMkFFM≪kFM。
FFM 模型学习
为了方便推导,这里省略FFM的一次项和常数项,公式为:

注意到∂Lerr∂ϕ∂Lerr∂ϕ和参数无关,每次更新模型时,只需要计算一次,之后直接调用结果即可。对于总共有dfkdfk个模型参数的计算来说,使用这种方式能极大提升运算效率。
第二个trick是FFM的学习率是随迭代次数变化的,具体的是采用AdaGrad算法,这里进行简单的介绍。
Adagrad算法能够在训练中自动的调整学习率,对于稀疏的参数增加学习率,而稠密的参数则降低学习率。因此,Adagrad非常适合处理稀疏数据。
设gt,jgt,j为第t轮第j个参数的梯度,则SGD和采用Adagrad的参数更新公式分别如下:
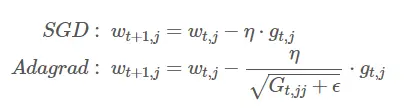
可以看出,Adagrad在学习率ηη上还除以一项√Gt,jj+ϵGt,jj+ϵ,这是什么意思呢?ϵϵ为平滑项,防止分母为0,Gt,jj=∑tι=1g2ι,jjGt,jj=∑ι=1tgι,jj2即Gt,jjGt,jj为对角矩阵,每个对角线位置j,jj,j的值为参数wjwj每一轮的平方和,可以看出,随着迭代的进行,每个参数的历史梯度累加到一起,使得每个参数的学习率逐渐减小。

实现的trick
除了上面提到的梯度分步计算和自适应学习率两个trick外,还有:
- OpenMP多核并行计算。OpenMP是用于共享内存并行系统的多处理器程序设计的编译方案,便于移植和多核扩展[12]。FFM的源码采用了OpenMP的API,对参数训练过程SGD进行了多线程扩展,支持多线程编译。因此,OpenMP技术极大地提高了FFM的训练效率和多核CPU的利用率。在训练模型时,输入的训练参数ns_threads指定了线程数量,一般设定为CPU的核心数,便于完全利用CPU资源。
- SSE3指令并行编程。SSE3全称为数据流单指令多数据扩展指令集3,是CPU对数据层并行的关键指令,主要用于多媒体和游戏的应用程序中[13]。SSE3指令采用128位的寄存器,同时操作4个单精度浮点数或整数。SSE3指令的功能非常类似于向量运算。例如,a和b采用SSE3指令相加(a和b分别包含4个数据),其功能是a种的4个元素与b中4个元素对应相加,得到4个相加后的值。采用SSE3指令后,向量运算的速度更加快捷,这对包含大量向量运算的FFM模型是非常有利的。
除了上面的技巧之外,FFM的实现中还有很多调优技巧需要探索。例如,代码是按field和特征的编号申请参数空间的,如果选取了非连续或过大的编号,就会造成大量的内存浪费;在每个样本中加入值为1的新特征,相当于引入了因子化的一次项,避免了缺少一次项带来的模型偏差等。
适用范围和使用技巧
在FFM原论文中,作者指出,FFM模型对于one-hot后类别特征十分有效,但是如果数据不够稀疏,可能相比其它模型提升没有稀疏的时候那么大,此外,对于数值型的数据效果不是特别的好。
在Github上有FFM的开源实现,要使用FFM模型,特征需要转化为“field_id:feature_id:value”格式,相比LibSVM的格式多了field_id,即特征所属的field的编号,feature_id是特征编号,value为特征的值。
此外,美团点评的文章中,提到了训练FFM时的一些注意事项:
第一,样本归一化。FFM默认是进行样本数据的归一化的 。若不进行归一化,很容易造成数据inf溢出,进而引起梯度计算的nan错误。因此,样本层面的数据是推荐进行归一化的。
第二,特征归一化。CTR/CVR模型采用了多种类型的源特征,包括数值型和categorical类型等。但是,categorical类编码后的特征取值只有0或1,较大的数值型特征会造成样本归一化后categorical类生成特征的值非常小,没有区分性。例如,一条用户-商品记录,用户为“男”性,商品的销量是5000个(假设其它特征的值为零),那么归一化后特征“sex=male”(性别为男)的值略小于0.0002,而“volume”(销量)的值近似为1。特征“sex=male”在这个样本中的作用几乎可以忽略不计,这是相当不合理的。因此,将源数值型特征的值归一化到[0,1]是非常必要的。
第三,省略零值特征。从FFM模型的表达式(3-1)可以看出,零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零,对于训练模型参数或者目标值预估是没有作用的。因此,可以省去零值特征,提高FFM模型训练和预测的速度,这也是稀疏样本采用FFM的显著优势。
参考: https://www.hrwhisper.me/machine-learning-fm-ffm-deepfm-deepffm/