常见反直觉定理
生日悖论
假设房间里有23人,那么两个人生日是同天的概率将大于50%。我们很容易得出,任何一个特定的日子里某人过生日的概率是1/365。
所以这个理论看似是无法成立,但理论与现实差异正源自于:我们的唯一要求是两个人彼此拥有同一天生日即可,不限定在特定的一天。 否则,如果换做某人在某特定日期生日,例如2月19日,那么23个人中概率便仅为6.12%。
另一方面如果你在有23个人的房间挑选一人问他:“有人和你同一天生日吗?”答案很可能是否定的。
但如果重复询问其余22人,每问一次,你便会有更大机会得到肯定答复,最终这个概率是50.7%。
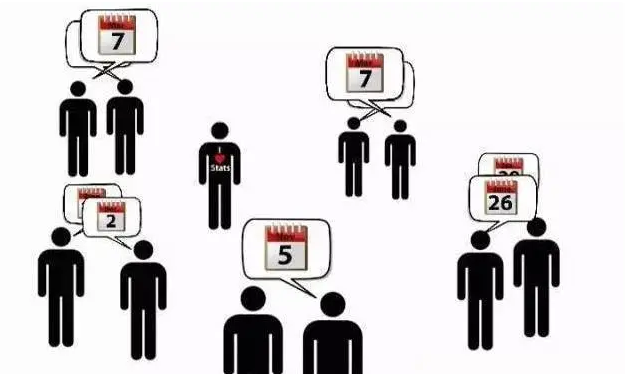
结论 当房间里有23人,那么存在生日相同的概率超过50%, 如果有60人,则超过99%
生日悖论的应用
- 日悖论普遍的应用于检测哈希函数:N 位长度的哈希表可能发生碰撞测试次数不是 2N 次而是只有 2N/2 次。这一结论被应用到破解密码哈希函数 (cryptographic hash function) 的 “生日攻击” 中。
- 生日问题所隐含的理论已经在 [Schnabel 1938] 名字叫做 “标记重捕法” (capture-recapture) 的统计试验得到应用,来估计湖里鱼的数量。
巴拿赫-塔尔斯基悖论(分球定理)
数学中,有一条极其基本的公理,叫做选择公理,许多数学内容都要基于这条定理才得以成立。
在1924年,数学家斯特·巴拿赫和阿尔弗莱德·塔斯基根据选择公理,得到一个奇怪的推论——分球定理。
该定理指出,一个三维实心球分成有限份,然后可以根据旋转和平移,组成和原来完全相同的两个实心球。没错,每一个和原来的一模一样。
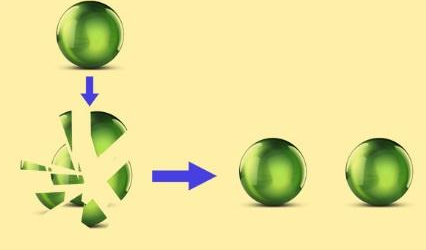 分球定理太违反直觉,但它就是选择公理的严格推论,而且不容置疑的,除非你抛弃选择公理,但数学家会为此付出更大的代价。
分球定理太违反直觉,但它就是选择公理的严格推论,而且不容置疑的,除非你抛弃选择公理,但数学家会为此付出更大的代价。
在现实生活中我们没有任何办法能将一个物体凭空复制成两个。但事实上他却是成立的,这个结果似乎挑战了物理中的质量守恒定律,但似乎又是在说一个物体的质量可以凭空变为原来的两倍?
但如若原质量是无限的话,翻倍后还是无限大,那么从这一层面出发来看这一理论也并没有打破物理法则。
有不同层次的无穷大(无穷大也有等级大小)
你可能从来想象不到,有一些无穷大比其他的无穷更大。无穷大应该被称为基数,并且一个无穷大如果比另一个无穷大拥有更大的基数,则说它比另一个无穷大要大。
在二十世纪以前,数学家们遇到无穷大都避而让之,认为要么哪里出了问题,要么结果是没有意义的。
直到1895年,康托尔建立超穷数理论,人们才得知无穷大也是有等级的,比如实数个数的无穷,就比整数个数的无穷的等级高。
 还有许多关于无穷大的基数大大出乎我们的意料。举一个非常经典的例子:整数比奇数多吗?你可能会毫不犹豫的回答,那是当然!
因为整数多出了一系列的偶数。但答案是否定的,他们拥有相同的基数,因而整数并不比奇数多。知道了这个道理,就不难回答这个问题了吧:有理数多于整数吗?不,有理数与整数相同多。
实数通常被认为是连续统,并且至今并能完全知道,是否有介于整数基数和连续统基数的无穷大?这个猜想被称为连续统猜想。
还有许多关于无穷大的基数大大出乎我们的意料。举一个非常经典的例子:整数比奇数多吗?你可能会毫不犹豫的回答,那是当然!
因为整数多出了一系列的偶数。但答案是否定的,他们拥有相同的基数,因而整数并不比奇数多。知道了这个道理,就不难回答这个问题了吧:有理数多于整数吗?不,有理数与整数相同多。
实数通常被认为是连续统,并且至今并能完全知道,是否有介于整数基数和连续统基数的无穷大?这个猜想被称为连续统猜想。
这也太违反直觉了,我们从来不把无穷大当作数,但是无穷大在超穷数理论中,却存在不同的等级。
哥德尔不完备定理
“可证”和“真”不是等价的
1931年,奥地利数学家哥德尔,提出一条震惊学术界的定理——哥德尔不完备定理。
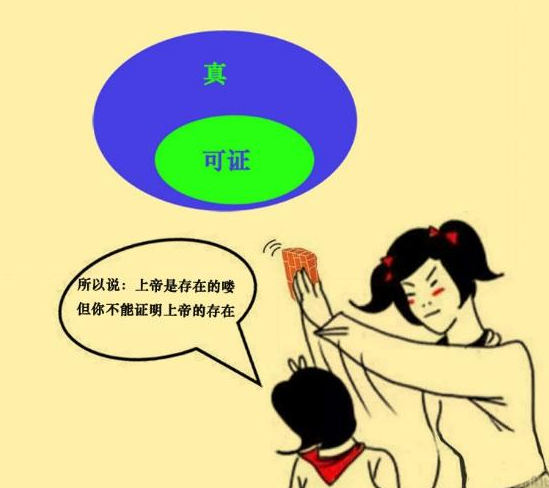 该定理指出,我们目前的数学系统中,必定存在不能被证明也不能被证伪的定理。该定理一出,就粉碎了数学家几千年的梦想——即建立完善的数学系统,从一些基本的公理出发,推导出一切数学的定理和公式。
该定理指出,我们目前的数学系统中,必定存在不能被证明也不能被证伪的定理。该定理一出,就粉碎了数学家几千年的梦想——即建立完善的数学系统,从一些基本的公理出发,推导出一切数学的定理和公式。
它的逻辑是这样的:
- 任何一个足够强的系统都存在一个命题,既不能被证明也不能被证伪(例如连续统假设)
- 任何一个足够强的系统都不能证明它自身是不推出矛盾,即便它不能被推出矛盾
以上两条定义即著名的哥德尔不完备定理。他的意义并不仅仅局限于数学,也给了我们深深地哲学启迪。
蒙提霍尔问题
三门问题亦称为蒙提霍尔问题,大致出自美国的电视游戏节目Let’s Make a Deal。问题名字来自该节目的主持人蒙提·霍尔。
参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。
当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。
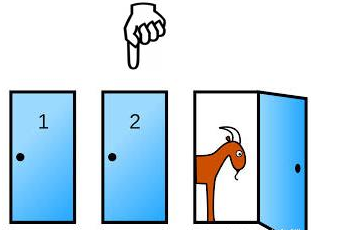 问题是:换另一扇门会否增加参赛者赢得汽车的机会率?
不换门的话,赢得汽车的几率是1/3。换门的话,赢得汽车的几率是2/3。
问题是:换另一扇门会否增加参赛者赢得汽车的机会率?
不换门的话,赢得汽车的几率是1/3。换门的话,赢得汽车的几率是2/3。
这个问题亦被叫做蒙提霍尔悖论:虽然该问题的答案在逻辑上并不自相矛盾,但十分违反直觉。
巴塞尔问题
将自然数各自平方取倒数加在一起等于π²/6。
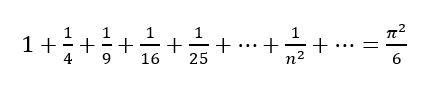 一般人都会觉得,左边这一坨自然数似乎和π(圆的周长与直径的比值)不会存在任何联系!然而它就这么发生了!
一般人都会觉得,左边这一坨自然数似乎和π(圆的周长与直径的比值)不会存在任何联系!然而它就这么发生了!
阿贝尔不可解定理
曼德勃罗集
德勃罗集是一个复数集,考虑函数f(z)=z²+c,c为复常数,在这为参数。
若从z=0开始不断的利用f(z)进行迭代,则凡是使得迭代结果不会跑向无穷大的c组成的集合被称为曼德勃罗集。规则不复杂,但你可能没预料到会得到这么复杂的图像。
 当你放大曼德勃罗集时,你会又发现无限个小的曼德勃罗集,其中每个又亦是如此…(这种性质是分形所特有的)
这真的很契合那句俗话“大中有大,小中有小”,下面有一个关于放大他的视频,我想这绝对令人兴奋不已。
当你放大曼德勃罗集时,你会又发现无限个小的曼德勃罗集,其中每个又亦是如此…(这种性质是分形所特有的)
这真的很契合那句俗话“大中有大,小中有小”,下面有一个关于放大他的视频,我想这绝对令人兴奋不已。

一维可以和二维甚至更高维度一一对应
按照我们的常识,二维比一维等级高,三维比四维等级高,比如线是一维的,所以线不能一一对应于面积。
但事实并非如此,康托尔证明了一维是可以一一对应高维的,也就是说一条线上的点,可以和一块面积甚至体积的点一一对应,或者说他们包含的点一样多。
 证明:
在1890年,意大利数学家皮亚诺,就发明了一个函数,使得函数在实轴[0,1]上的取值,可以一一对应于单位正方形上的所有点,这条曲线叫做皮亚诺曲线。
证明:
在1890年,意大利数学家皮亚诺,就发明了一个函数,使得函数在实轴[0,1]上的取值,可以一一对应于单位正方形上的所有点,这条曲线叫做皮亚诺曲线。
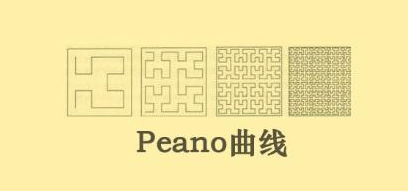 这个性质的发现,暗示着人类对维度的主观认识,很可能是存在缺陷的。
这个性质的发现,暗示着人类对维度的主观认识,很可能是存在缺陷的。
希尔伯特的旅店
 希尔伯特有一个旅店,旅店里有无限多间房间。有一天所有房间都住满了人。然后又来了一名旅客。希尔伯特说:很抱歉,房间都住满了。旅客说:没关系。你可以让第一间房间的人住第二间房,第二间房间的人住第三间房,如此类推,我就可以住第一间房间了。也可以让第一间房间的人住第二间房,第二间房间的人住第四间房,以此类推,我也可以住第一间房间。
希尔伯特有一个旅店,旅店里有无限多间房间。有一天所有房间都住满了人。然后又来了一名旅客。希尔伯特说:很抱歉,房间都住满了。旅客说:没关系。你可以让第一间房间的人住第二间房,第二间房间的人住第三间房,如此类推,我就可以住第一间房间了。也可以让第一间房间的人住第二间房,第二间房间的人住第四间房,以此类推,我也可以住第一间房间。
甚至,按照这种做法,无论再来多少客人,只要客人是有限个,这个住满的酒店都可以继续空出房间来给他们安排。 他的说法很反直觉,但是从数学角度上,他是正确的。
为了讨论这个问题,我们首先要问:全体正整数和全体正偶数谁多? 大部分人的直觉都是:整数多。因为整数包含奇数和偶数,所以整数多。
但是,正整数集合和正偶数集合都是无限多个元素。在数学上,无限多个元素的集合比较多少时要使用“势”的概念。也就是:如果两个集合可以建立一个一一对应的关系,那么这两个集合的元素个数就是一样多的。 所以,如果我们令x表示正整数,y表示正偶数,建立对应关系y=2x,那么正整数和正偶数之间就建立了一一对应的关系,所以正整数集合和正偶数集合是等势的,或者说全体正整数和全体正偶数一样多。 按照这种观点,我们可以继而可以证明全体正整数数和全体非负整数一样多:建立一一对应关系:y=x-1,x属于正整数,y属于非负整数。 所以,客人来到希尔伯特的酒店住宿,提出的两种方案都是合理的。第一种方案基于全体正整数(房间)和全体非负整数(客人)是一样多的,第二种方案是基于全体正偶数(房间)和全体正整数(客人)是一样多的。
有理点
我们把平面上横坐标和纵坐标都为有理数的点称为 有理点.
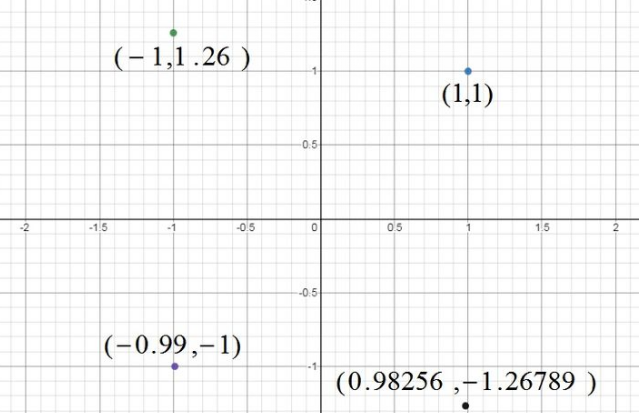 显然,平面上的有理点有无穷多个,甚至不难证明它们在整个平面内是稠密的,即密密麻麻地铺满了整个平面. 设想一下,如果我们在平面上随手画一条曲线,直觉上我们可能认为这根曲线应该会经过无限多个有理点,也就是说曲线上有无限多个有理点.
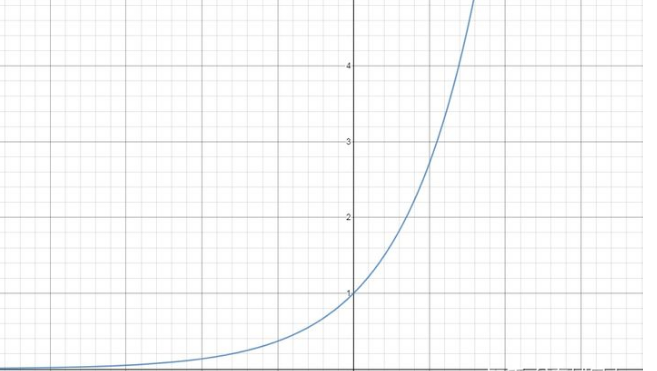
但事实上并非一定如此!比如我们非常熟悉的曲线 y=e^x,它除了(0, 1)外没有其他任何有理点,也就是说它非常神奇地避开了处处稠密的有理点,这就挺反直觉的.
显然,平面上的有理点有无穷多个,甚至不难证明它们在整个平面内是稠密的,即密密麻麻地铺满了整个平面. 设想一下,如果我们在平面上随手画一条曲线,直觉上我们可能认为这根曲线应该会经过无限多个有理点,也就是说曲线上有无限多个有理点.
但事实上并非一定如此!比如我们非常熟悉的曲线 y=e^x,它除了(0, 1)外没有其他任何有理点,也就是说它非常神奇地避开了处处稠密的有理点,这就挺反直觉的.
买彩票
买彩票中奖的概率问题。同一天内买30注不同的号码中一等奖概率高还是连续30期每次买一注至少有一次中大奖的概率高。我想当然得人为是后者概率高,但是实际上经过计算后,是前者概率高,并且两者的中奖奖金期望值是相同的。